Algorithme de Dijkstra

Maths

In : $G=(N,R)$ un graphe orienté pondéré avec des poids positifs et $s\in N$

Out : Une liste de taille $|N|$ contenant les distances minimales séparant $s$ de tous les autres nœuds.

Init : Soit $N_s:=\{s\},\overline{N_s}:=N-N_s$ et, $d(u):=c(s,u)\forall u\in N$ ($d(u)=\infty$ si il n'y a pas d'arête entre $s$ et $u$). (où $c(s,u)$ est le poids de l'arête reliant $s$ et $u$).

Loop : Tant que $\overline{N_s}\ne \varnothing$ :

• $v:=$ un élément de $\overline{N_s}$ qui minimise $d(v)$
• $N_s:=N_s\cup \{v\}$ (et $\overline{N_s}:=N-N_s$)
• $\forall i\in \overline{N_s}:d(i):=\text{min}(d(i),d(v)+c(v,i))$

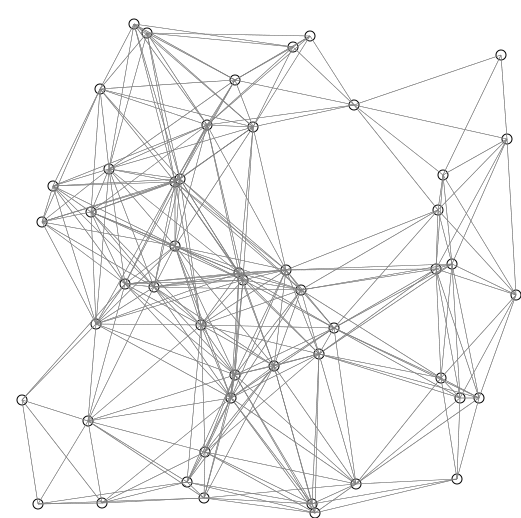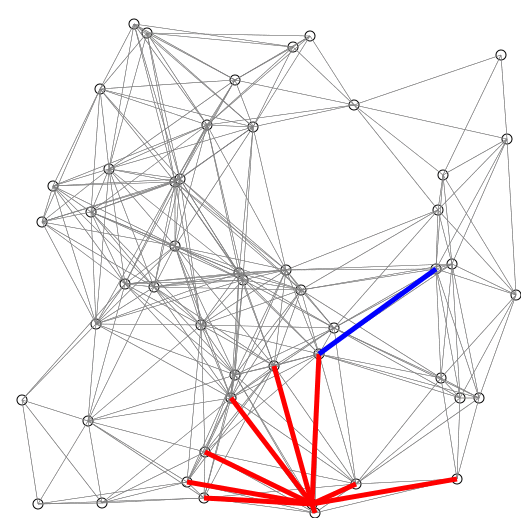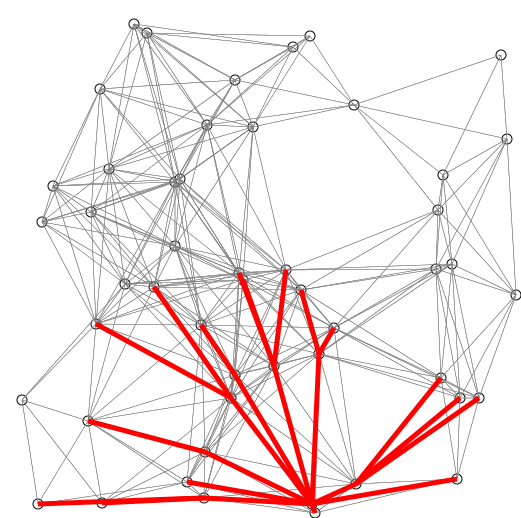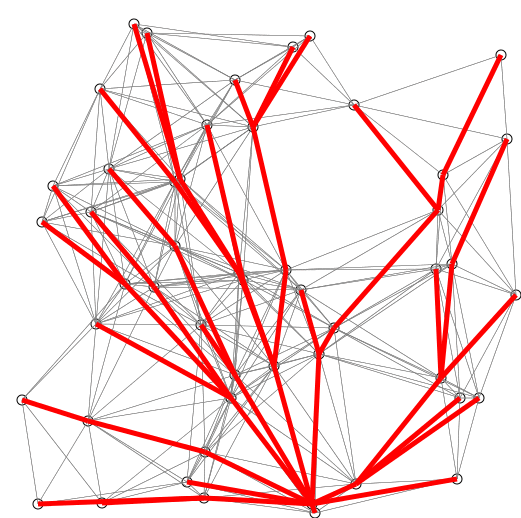
Description

1. On créé la liste $d$ de taille $|N|$ qu'on initialise à 0 pour $d(s)$, $c(s,u)$ pour les nœuds adjacents à $s$ et $\infty$ pour les autres nœuds. On créé également l'ensemble $N_s$ qui contient les nœuds dont on connait la distance minimale ainsi que l'ensemble $\overline{N_s}$ qui contient les nœuds restants.
2. Tant que $\overline{N_s}$ n'est pas vide ou tant que $|N_s|\ne |N|$ on répète la procédure suivante :
3. On prends l'élément $u$ de $\overline{N_s}$ qui est le plus proche de $s$, on le retire de $\overline{N_s}$ et on le place dans $N_s$. Ensuite on regarde pour tous les nœuds restants dans $\overline{N_s}$ si la valeur de leur distance dans $d$ peut être raccourcie en prenant $d(u)$ plus le poids associé à l'arête séparant $u$ et le nœud en question
4. $d$ contient les valeurs recherchées.

Implémentation Python

def dijkstra(graph, source):
    dist = {vertex: float('infinity') for vertex in graph.vertices}
    dist[source] = 0
    
    Q = set(graph.vertices)
    
    while Q:
        u = float('infinity')
	    for vertex in Q:
		    u = min(u, dist(vertex))
        Q.remove(u)
        
        for v, weight in graph.edges.get(u, {}).items():
            if v in Q:
                alt = dist[u] + weight
                if alt < dist[v]:
                    dist[v] = alt
    
    return dist

Complexité

Implémentation naïve :

Spatiale : $O(|N|)$

Temporelle : $O(|N{|}^2+|R|)$

Meilleure Implémentation

Temporelle : $O(|R|+|N|\log |N|)$ Voir : Tas de Fibonacci

Preuve de validité

Todo